Methods for delineating difference boundaries are called wombling techniques, after Womble (1951). Womble quantified the spatial rate of change by estimating surface gradients in a raster structure. Differences among wombling methods are mostly related to data format (vector, raster, or transect), data type (numeric or categorical), and boundary type (crisp or fuzzy).
Boundary Likelihood Values (BLVs) measure the spatial rate of change. Locations where variable values change rapidly are more likely to be part of a boundary; these locations have higher BLVs. For numeric data in point or raster format, BoundarySeer calculates BLVs from gradient magnitudes for the suite of variables. BoundarySeer uses dissimilarity metrics for categorical and polygon data.
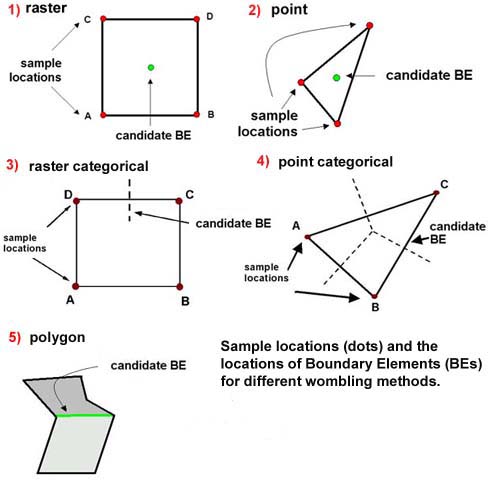
The locations that have the highest BLV values are Boundary Elements (BEs), considered part of the boundary. The location of candidate BEs depends on the specific boundary delineation technique employed (see figure below).

Candidate BEs become part of the boundary when their BLVs exceed established thresholds. In crisp wombling, those BLVs with values above the threshold are assigned a Boundary Membership Value (BMV) of 1 (non-BEs have BMV = 0). In fuzzy wombling, BMVs can range between 0 and 1 and indicate partial membership in the boundary. Determining BMVs for fuzzy boundaries is described in Crisp vs. fuzzy wombled boundaries.
The next step in delineating crisp difference boundaries is to connect BEs to create subboundaries. BoundarySeer evaluates subboundaries between pairs of BEs using a few decision rules. First, for all wombling methods, BEs are connected only if they are adjacent. With irregular (point) and raster wombling, connection is based on the gradient angle of two adjacent BEs (see constructing subboundaries).
Fuzzy boundaries are not connected to form subboundaries, so determination of the Boundary Membership Value for each BLV location is the end of the fuzzy wombling process.
As wombling methods and BLV calculations are specific to each data type, see the following topics for specific information: Raster wombling, Point wombling, Categorical wombling, and Polygon wombling.
See also: