
Boundaries may be precise or imprecise. BoundarySeer allows you to choose how you represent the boundaries in your data set by offering both precise (crisp) and imprecise (fuzzy) boundary options when you use the various wombling techniques. Crisp boundaries can be thought of as distinct zones of change - they are often represented by distinct lines that separate various regions of the data. Fuzzy boundaries are represented as broader regions of change, with some areas appearing more important in determining the boundary than others (see figure below).

An example of a fuzzy boundary
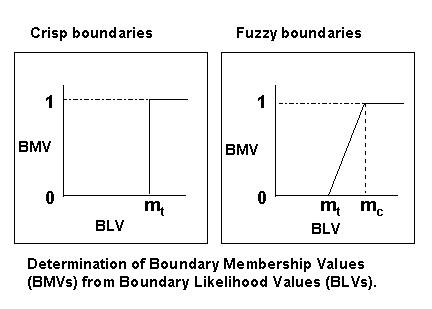
For crisp boundaries, the Boundary Elements are determined by finding which locations have Boundary Likelihood Values (BLVs) above some pre-set threshold, such as the top 30%. Those BLV locations with values above the threshold are assigned a Boundary Membership Value (BMV) of "1", and appear as boundary elements in boundary data sets. Those BLV locations that fall below the threshold are assigned a BMV of "0", and are not an element of the boundary data set (see figure below - the value "mt" is the user-set threshold).
Fuzzy boundaries are determined by a slightly different process. BoundarySeer sets a range of BMVs using BLV thresholds for the boundary (mt) and boundary core (mc; see figure below). Locations with BLVs below the boundary cutoff are not part of the boundary (BMV = 0). Locations with BLVs above the boundary threshold but below the core threshold are part of the fuzzy boundary (0 < BMV < 1). Locations with BLVs above the core threshold are the core of the boundary (BMV = 1).
Crisp boundaries may be represented as an ordinary set by enumeration, written B {(x1, y1),...(xNB, yNB)}. The members of the set are the boundary elements, or BEs. Here NB is the number of locations in the boundary. The underscore notation indicates that B is an ordinary set, in that a given location (xi, yi) is either a member of the set or it is not, and membership in the set is said to be certain. Such ordinary boundaries can be written either by enumeration or as a function that defines a mapping (f) from X,Y to the values 0 or 1 (Zadeh 1965, Leung 1987), using a characteristic function f(x,y) that defines the degree of membership of (x,y) in B (see equation below).
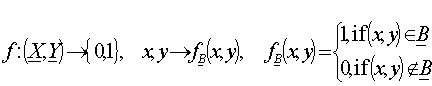
Imprecision can cause membership in boundaries to be uncertain, and this uncertainty may be represented using fuzzy subsets. A fuzzy boundary (written B, no underscore) is a set of ordered pairs [(xi,yi), µB(xi,yi)] where all x,y are elements of the universe of discourse X, Y, and µB(xi,yi) is the degree of membership of location (x,y) in the fuzzy boundary B. 'Fuzzy' means that µB(xi,yi) lies on the interval (0,1). Notice the universe of discourse is the real numbers and is precise. B is called a fuzzy boundary because it is membership in B that is fuzzy.
See also: