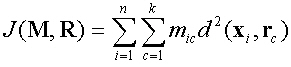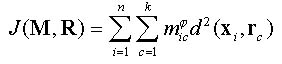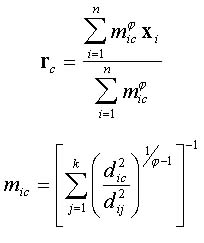About k-means clustering

K-means clustering is an algorithm that is used in two different BoundarySeer techniques, spatially-constrained clustering and fuzzy classification.

Both techniques require grouping the data into classes, or clusters. In fuzzy classification, the classes are based on variable values, irrespective of spatial location. In spatially-constrained clustering, as the name suggests, group membership is constrained by the spatial location, i.e. distant locations with similar values will not be grouped together.

For both methods, k-means clustering begins and ends with a fixed number of classes (or clusters). Class memberships are rearranged through an iterative process in order to optimize the classification, using the following criteria:

Method	Spatially constrained clustering	Fuzzy classification
# groups	k clusters	k classes
spatial constraint	spatial contiguity	none
dissimilarity metric	squared Euclidean distance	squared Euclidean distance
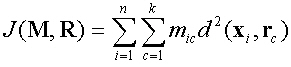
refinement criterion	minimize within-cluster variation using the sum of squares error term (SSE)	minimize within-class variation using the sum of squares error term (SSE) (after Bezdek et al. 1984)
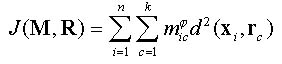
refinement method	At each iteration, all locations that can change cluster membership are identified. To qualify for a change of membership to a new cluster, a location must be adjacent to a member of the new cluster, and its removal from its former cluster cannot cause the former cluster to become discontinuous. The membership change that causes the greatest decrease in the total within-cluster SSE is then made. The process repeats until no allowable membership relocation improves the SSE.	When f > 1, J can be minimized by Picard iteration of the following equations:

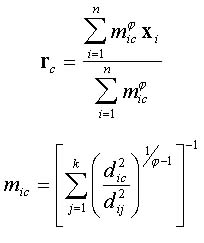
Where, M = (mic) is a matrix of class memberships,
R = (rcv) is a matrix of class means, rcv, denoting the mean of class c for variable v,
xi = (xi1,...,xip)T is the vector representing values of the p variables at location i,
rc = (rc1,...,rcp)T is the vector representing the center of class c in terms of means of the p variables,
d2(xi,rc) is the square distance between xi and rc, also expressed as dic2.
f is the fuzziness criterion ( f= 1 gives hard clusters and is required for spatially constrained clustering; f= 2 is a good minimum value for fuzzy clustering McBratney and de Gruijter 1993).
e is the stopping criterion, which determines the level of convergence necessary before quitting (McBratney and de Gruijter 1993 recommend e = 0.001).

See also: