Implementation of Poisson Regression

As described here in the overview of Poisson regression, the goal of this statistical tool is to parameterize a relationship between one or more independent variables, and the expected value (mean) of a discrete (integers only) dependent variable that follows a Poisson distribution.  This statistical tool uses the log as its link function; taking the log of the function produces a linear combination of predictors, so again this is a form of linear model.  The log link funtion also constrains the expected values to positive numbers.  As shown in the overview of Poisson regression, a general formula can be written as:

Obtaining the parameter estimates

For  regression in SpaceStat, the regression formulation is carried out in terms of maximum likelihood (L) estimation.  A "likelihood" is a probability (and must be have a value within the range of 0 - 1); in this case the probability that the dependent variable can be predicted from the independent variables.  As indicated in the equation below, the maximum likelihood estimator uses a Poisson distribution to define a joint probability distribution from the individual dependent variable observations.   In the following equations, the brackets around the beta, which symbolizes the regression coefficients, indicate that we are estimating two or more regression coefficients.

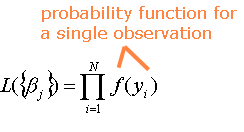
The goal of maximum likelihood estimation is to maximize the Log-Likelihood (lnL), which has a value between 0 and negative infinity (negative, because you are taking the log of a value that is less than 1). Maximum likelihood estimation is an iterative process.  Recall also from our overview that we are treating aspatial regression as a the "global" version of geographically-weighted regression; as a result, we need to account for weighting factors (w) in our estimation.  The weighted log-likelihoods for logistic regression can be obtained by raising each individual probability to the power of a weight factor, taking the product over observations, and then taking the logarithm.

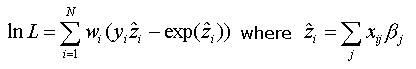
To estimate the regression coefficients, SpaceStat uses the Taylor expansion of the equation above, and then the maximum likelihood algorithm determines the direction and sign of changes in the regression coefficients which will increase the lnL.  After starting from an arbitrary set of coefficient estimates, the initial function is estimated and the residuals are evaluated.  From these results, the algorithm modifies the coefficient values, and generates a new set of residuals which are compared to previous values.  This process continues until there is little change in the lnL. There is a possibility that this process will not lead to convergence due to what is called a "ridge-effect"; in this case, the Log-Likelihood stays constant as coefficients are varied.

Evaluating the full model

To evaluate the significance of the full Poisson regression model, SpaceStat presents the difference (deviance) between the log-likelihood of the full model and that of a "perfectly-fitted" model in which the Poisson mean at each observation is set equal to the observed value. The deviance is divided by the number of degrees of freedom and this quotient is then compared with unity to judge the goodness of fit.  An example of the output table showing the deviance value is shown here.  Values for deviance/DF that are greater than 1 indicate that the variance is larger than the mean (overdispersion), while values smaller than one suggest the true variance is smaller than the mean (underdispersion).  Strong evidence of either over- or underdispersion suggests that a Poisson model is not a good fit for your data.

Significance of individual terms in the Poisson regression model

For Poisson regression, SpaceStat presents the parameter estimates, parameter standard errors and p-values (using a chi-squared distribution); click here to see an example.  Likelihood ratio tests are used to evaluate the significance of individual parameters in the model.  The basic idea of these significance tests is the same as the test of significance of the full model, except the tests are based on the difference in -2lnL for an overall model and a nested model where one term has been dropped.  If the test for a particular parameter is not significant, this means that coefficient for that variable can be considered to not be significantly different from zero, and that you can drop this variable from your model without a reduction in model performance.