Categorical Data in Regression Analyses
It is relatively straightforward to understand regression using continuous independent variables: For example a simple aspatial linear regression model involves finding the best fit of a straight line through a set of points in the x-y plane, fitting a single intercept and slope. A simple GWR model would repeat this approach across multiple overlapping neighborhoods in a spatial dataset, but would still be fitting a single intercept and slope to these subsets of the data. However, regression using categorical dependent variables differs in that a different regression parameter must be chosen for each of the categories represented in a categorical dataset. Details related to this process of coding of categorical variables are described below. Note that for SpaceStat to recognize a dataset as categorical, it must be a string (alphanumeric) dataset type.
Reference cell vs. Effect cell parameterization
In SpaceStat, there are two options for handling how categorical variables are coded for parameterization of the coefficients; reference cell and effect cell parameterization. Both options link the different regression coefficients to individual on-off variables for each of the categories within the categorical dataset. Using reference cell parameterization for a variable with three categories would introduce two indicator or "dummy" variables that take either the value zero or one for the first two categorical values. Specifically, one category would be coded "0 1" and a second would be "1 0", and both indicator variables (codes) would be zero for the third category (0 0). This final code (0 0) is assigned to the category chosen to be the reference cell (see below). Note that with either reference cell or effect cell coding, your code will always have the same number of digits as your degrees of freedom (the number of categories minus 1). For example, in a dataset with four categories, the reference cell would be coded "0 0 0" rather than "0 0".
As shown here in the SpaceStat interface for aspatial linear regression, when you run a regression with categorical data, you will need to pick which category will be the reference cell. A regression model with an intercept and an independent variable with three categories would then have a total of 3 coefficients (1 for the reference cell, which acts as the intercept, and two for the categories with codes that include 1), and the resulting matrix of values that SpaceStat uses to estimate coefficients would avoid the problem of singularity. The second coding option, effect–cell coding, assigns the values -1 for each of the two variables when data lie in the third category, so the three possible codes expressed with the two coding variables are 0 1, 1 0, and -1 -1). Again, this coding avoids the problem of having too many parameters in the matrix used to perform the maximum likelihood estimation.
The choice of coding depends upon the goals of your analysis. To give a very simple example, say you are trying to predict your dependent variable "y" using just the independent variable "gender" in an aspatial linear model. Working with the traditional linear regression equation, you would have:
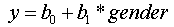
If you picked reference cell coding, and chose males as the reference value (i.e., the category coded as 0), then for females your dependent variable would equal b0 + b1, while for males y would equal just b0, because multiplying the b1 by zero would cause it to drop out. In effect, the y values are the means for each of the two categories, and a t-test (i.e., a two sample F-test) for b1 will test the hypothesis that the mean for females is significantly different from the mean for males. Alternatively, if you picked effect cell coding, then if you chose males as the reference cell, they would be coded -1, and females would be coded 1. For females, your dependent variable would still equal b0 + b 1, but the y for males would equal b0 - b1. You would still end up with the result being the mean of each category, but your significance test for the coefficient associated with each categorical level would test the hypothesis that the mean for females is significantly different from the mean for the WHOLE GROUP (males plus females).
Categorical variables in model selection (stepwise regression)
Even though SpaceStat creates an indicator variable for each category in a categorical dataset, the dataset is treated as one unit in the model selection procedures (e.g., forward and backward stepwise regression, best model selection). This means that categorical variables, or interaction terms that include categorical variables, will drop or add the entire variable or interaction term and evaluate changes in model fit, rather than dropping one categorical level at a time. When you are using these tools, you will still be able to choose between reference cell and effect cell parameterization.
Complications with models that include categorical variables
Complications arise with the parameterization of regression coefficients when combinations of categorical variables are used in the regression model. Suppose you wish to model the weight of a cat or dog using (a) gender (b) animal type, and (c) the combination (interaction) of gender and animal type. For the interaction term, SpaceStat would parameterize the four possible combinations of categories using an intercept and three on-off variables with the fourth (e.g., male*dog) as a reference value. However, trying to parameterize this model with two variables, and the interaction term would lead to five parameters for only four categories, and a regression matrix where the entries in one column are always equal to the sum of the entries in two other columns.
A similar problem arises when the regression model involves the product of categorical and continuous variables, for example animal weight versus the product of animal type (cat or dog) and height. In this case the reference cell parameterization would only allow a non-zero slope for one of the two animal types since the reference value does not have a variable assigned to it. Therefore, for products of categorical and continuous variables, the categorical reference value has to be reintroduced so that a linear dependence on height can be allowed for that category. Again if you tried to model regression against both the height, and the product of height and animal type, then over-parameterization would occur and SpaceStat will flag the regression model as having a singular regression matrix.
Here's the bottom line: Don't define a model with categorical linear variables in combination with a fully categorical interaction term, and don't use the same continuous variable as a linear term and in an interaction with a categorical term.
Details on the handling of overparameterized models
When the model that you have defined includes too many parameters (and regression matrix inversion fails because the regression matrix is singular), SpaceStat adopts the procedure of trimming the model of excess parameters so that you can obtain valid estimates of the dependent variable and its standard error. Specifically, the Singular Valued Decomposition (SVD) procedure is used to obtain the number of singular elements in the regression matrix, as well as lists of parameters that are linearly related to each other. The parameters at the end of each list are then removed and the regression matrix is tested again to ensure that the number of singular elements has been reduced. The procedure is then repeated until no more singularities remain in the regression matrices.
For a singular regression matrix, the SVD procedure does not produce the only valid estimates of the dependent variable. Other combinations of the regression model coefficients that are linearly dependent on each other could be removed just as well - consequently the reduced model parameterization is not unique. Therefore the Type III ANOVA results (presented for aspatial regression) will represent the sum of squares for an arbitrarily reduced model and should not be regarded as unique.