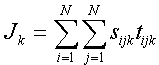
|
Ho |
Whether cases are nearest neighbors in space is independent of whether they are nearest neighbors in time |
|
Ha |
Nearest neighbors in space tend to be nearest neighbors in time. |
The test statistic, Jk, is the count of the number of case pairs that are k nearest neighbors in both space and time. When space-time interaction exists Jk will be large, since nearest neighbors in space will also tend to be nearest neighbors in time.
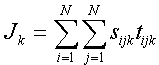
k is the number of nearest neighbors to consider in the analysis (if k=1, consider the first nearest neighbor; if k=2 consider the first and second nearest neighbors).
sijk is the spatial nearest neighbor (NN) measure, sijk =1 if case j is a k NN of case i in space, and 0 otherwise.
tijk is the time NN measure, tijk =1 if case j is a k NN of case i in time, and 0 otherwise.
The Jk are not independent because case pairs counted as nearest neighbors when k is small are included in when higher numbers of neighbors are considered. For example, J2 is the count of the number of pairs that are second nearest neighbors in both space and time, and includes all case pairs that were first space-time nearest neighbors. DJk is the number of space-time nearest neighbors added by increasing k by 1. DJk measures space-time interaction above and beyond that observed for the k-1 nearest neighbors. Jk, on the other hand, is a cumulative measure of space-time interaction where all nearest neighbor relationships from 1 up to k are included.
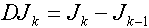
ClusterSeer evaluates the significance of Jk using an approximate randomization of the Mantel product. Let Sk denote the matrix of spatial nearest neighbor measures (the sijk), and let Tk denote the matrix of time nearest neighbor measures. P-values are calculated by comparing the observed Jk to the distribution of Jk obtained under Monte Carlo randomization. The elements of Tk are shuffled by permuting its rows and columns and Jk is then calculated. This procedure is repeated a fixed number of times, resulting in a distribution of Jk under the null hypothesis of no association between the space and time nearest neighbor relationships.