Empirical Bayesian Smoothing

Empirical Bayesian smoothing takes the population in the region as an indicator of confidence in the data, with higher population providing a higher confidence in the value at that location.

The empirical Bayesian smoother is one tool for dealing with rate instability associated with small sample sizes, and is described in detail in Waller and Gotway (2004). In SpaceStat, the smoother takes a rate dataset and a population-at-risk dataset and uses them to create three new datasets: two smoothed rate datasets (one using the local and one using the global mean) and a dataset of the local means. The smoothed datasets are calculated by the following formula:

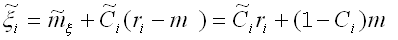
Where 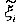is the new smoothed rate estimate, m is the global (r) or local (ri) population-weighted mean, C is the shrinkage factor, and r is the rate dataset.

Shrinkage factor

The shrinkage factor sets the relative importance of the observed value versus the expected value, which is either the global or the local mean. Terms are as defined above, and s2 is the global or local sample variance.

When the population size, ni, is small, the shrinkage factor is near zero, and the estimated value is very close to the global or local mean. When the population size is large, the shrinkage factor is near 1 and the Bayesian smoother returns a value near the observed value.

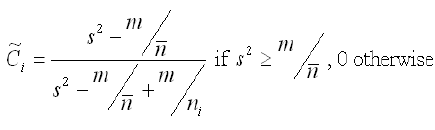
Missing values

The estimate will be missing for the local smoother if the local mean cannot be calculated, due to missing population or missing rate values.