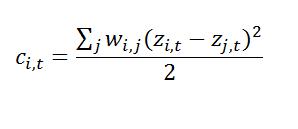Geary's C statistic

H_o	There is no association between the value observed at a location and values observed at nearby sites: values of ci are close to one.
H_a	Nearby sites have either similar (ci is close to 0) or dissimilar values (ci is greater than 1).

Formally, Geary's c is:

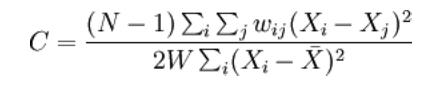
where N is the number of observations, wij is the spatial weight corresponding to the observation pair (i, j), Xi and Xj are observations for locations i and j (with mean 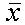) and W is a scaling constant such that,

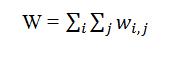
(ie, the sum of all weights).

Under the null hypothesis of no spatial autocorrelation the expected value for Geary’s C is 1. A value of Geary's C which is less than 1 indicates positive spatial autocorrelation, while a value larger than 1 points to negative spatial autocorrelation. Note that c is always non-negative.

Test statistic at the local level

We define the local c statistic as follows.

	zi,t is the z-score standardized dataset being tested for region i at time t
	zj,t is the z-score standardized dataset for region j at time t
	wij is a spatial weight set denoting the strength of connection between areas i and j

Our definition differs from Anselin (1994) by a factor of 2. This ensures the expected value of the local statistic under the null hypothesis is 1, as for the global statistic, and can be interpreted similarly. Thus, a local ci,t statistic close to 1 indicates that there is no significant autocorrelation between observation i and its neighbors, where ci < 1 indicates that the observation has neighbors which are significantly similar to it (positive spatial autocorrelation). Likewise, ci > 1, demonstrates that the observation is among neighbors which differ significantly from it (negative spatial autocorrelation). SpaceStat evaluates the significance of Local Geary’s statistic values with Monte Carlo randomizations, using conditional randomization.

The impact of missing values in Geary’s C analyses

Spatial weight sets are independent of the values in the geography's datasets, including missing values. If you have a dataset with missing values, calculations of the Geary’s C statistics will be based only on those neighboring locations with data. SpaceStat will not substitute another neighbor for the location with the missing value. The statistics are evaluated for significance with Monte Carlo randomizations (i.e, the differences in the distribution of observed statistic values can influences whether a particular value is judged as "rare"). Removing one or more locations from a geography (thus creating missing values) can change results for all locations. You might observe this if you decide that a value or two represent outliers in your data, and re-run an analysis using missing values instead of the recorded ones. You will find that results for locations close to the one where missing values now occur change, but results for other locations may change as well due to the change in the overall distribution of ci.