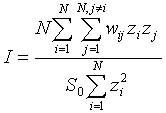
|
Ho |
Disease rates are spatially independent, the observed rates are assigned at random among locations. I is close to zero, depending on sample size. |
|
Ha |
Disease rates are not spatially independent. I is not zero. |
Moran's I (Moran 1950) is a weighted correlation coefficient used to detect departures from spatial randomness. Moran's I is used to determine whether neighboring areas are more similar than would be expected under the null hypothesis. Moran's I is:
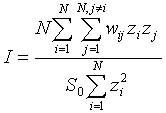
where N equals the number of regions, wij is a weight denoting the strength of the connection between areas i and j, zi is the rate in region i centered about the mean rate (using zi = xi – ave(x); xi is the rate in region i); and So is the sum of the weights

The variance under assumption N is:The expectation of I under the null hypothesis is:
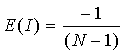
The expectation becomes close to 0 as N increases. The variance of I is determined under two null hypotheses or assumptions: Normality (denoted N) or randomization (denoted R). Under assumption N the rates are sampled from a population whose distribution is normal. Under assumption R the rates are random samples from a population whose distribution is unknown. Assumption N is useful when we have good reason to believe the observations follow a normal distribution. Assumption R is less restrictive and, since we often don’t know their theoretical distribution, is appropriate for disease rates. The variance under assumption N is:
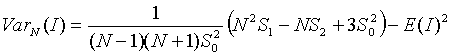
Under the assumption R the variance is:
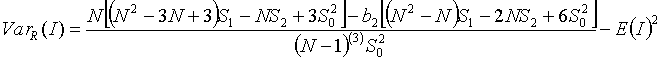
where a falling factorial is written s(b)=s(s-1)…(s-b+1),

Significance
ClusterSeer calculates significance values and z-scores to help you evaluate the significance of the test statistic.